丑数

我们把只包含因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

*说明: *

1. 1 是丑数。
2. n 不超过1690。

丑数的递推性质： 丑数只包含因子 2,3,52, 3, 5 2, 3,5 ，因此有 “丑数 == = 某较小丑数 ×\times × 某因子” （例如：10=5×210 = 5 \times 2 10= 5× 2 ）。

丑数的递推性质： 丑数只包含因子 2, 3, 52,3,5 ，因此有 “丑数 == 某较小丑数 \times× 某因子” （例如：10 = 5 \times 210=5×2）。

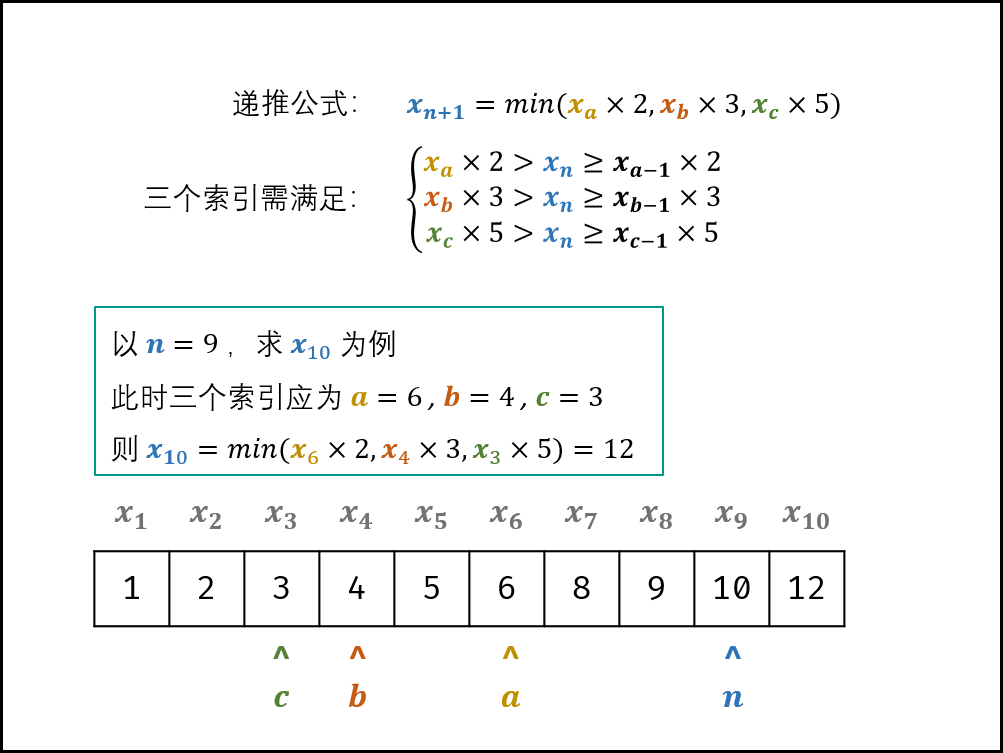
作者：jyd
链接：https://leetcode-cn.com/problems/chou-shu-lcof/solution/mian-shi-ti-49-chou-shu-dong-tai-gui-hua-qing-xi-t/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

//丑数的递推性质： 丑数只包含因子 2, 3, 52,3,5 ，因此有 “丑数 == 某较小丑数 \times× 某因子” （例如：10 = 5 \times 210=5×2）。
public int nthUglyNumber(int n) {
    int[] dp = new int[n];
    dp[0] = 1;
    //用a,b,c 标记分别*2，*3，*5的数
    //因为可能存在先加入了比较大的数,所以不能直接按顺序加入。分别标记上一次用了谁
    int a=0, b=0, c = 0;
    for (int i = 1; i < n; i++) {
        int numA = dp[a] * 2;
        int numB = dp[b] * 3;
        int numC = dp[c] * 5;
        //保证了当期那添加的是最小的
        dp[i] = Math.min(numA, Math.min(numB, numC));

        //可能会存在相等的情况，都加
        if(dp[i] == numA) a++;
        if(dp[i] == numB) b++;
        if(dp[i] == numC) c++;
    }
    return dp[n-1];
}